乐谱基础知识《第八讲 音程》教程

音程
在音乐体系众多的音。音与音之间的关系叫音程。（实际上就是两个音之间的“距离”）。
音程中的两个音，各自都有自己的名称，低音叫做“根音”（也叫下方音）、高音叫做“冠音”（也叫做上方音）。
一 曲调音程
“根音”与“冠音”先后发出的关系，叫做“曲调音程”（也叫旋律音程）。
谱例1：

曲调音程分别有“上行”、“下行”、和“平行”。在谱面上书写要根据发音的先后次序来书写。
谱例2：

二 和声音程
“根音”和“冠音”同时发出声音叫做“和声音程”。
谱例3：

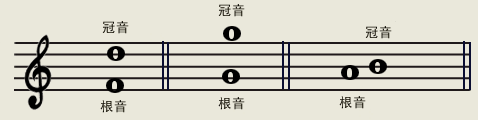
和声音程在谱面上标画的时候上下两个音一定要对齐。（注：二度音是不能对齐的，也对不齐，只能错开写，但是应该低音在左边，高音在右边。）
三 音程的读法
上行的曲调音程与和声音程都要从低读到高（也就是从根音读到冠音）。而下行的曲调音程和平行的的曲调音程一定要读出走向。比如说：从G到下面的B，或者是从E平行到E，等等 。
1 度数
在我们日常生活当中，有很多的计量单位。比如说量长度的有公里、米、厘米、尺、寸，重量单位有斤、两等等。
音程同样也有一个度量单位，这就是“度”，也叫做“度数”。
其中还包含着“音”也叫做“音数”。音程的大小名称都是由“度数”和“音数”决定的。
五线谱上的每一条线和每一个间都是一度。两个音同在一条线上，或者同在一个间里的时候，这两个音的音程关系叫做“一度”，或者叫做：“同度”。
如果两个音，一个在线上，另一个音在紧挨这个音的间里，那末这两个音之间的音程关系叫做：“二度”。
如果两个音都在线上，而且是最近的两条线上，或者是两个音同样在两条最近的间里，这两个音之间的音程关系就叫做：“三度”。就是音程的度数。也就是两个音中间相距有多少个音级。
谱例1：


2 音数
音程的构成，除了“度数”还包含有“音数”。
音数是指两个音级之间包含着多少个半音。
音数是由分数来表示的： “1”表示是全音、“1/2”表示是半音、“1.1/2”表示一个全音加上一个半音。
辨别音程的关系，就是要根据两音之间的“度数”和两音之间包含的“音数来确定，为了音程的完整性，我们还需要在“度数”和“音数”的前面再加说明性的五个字：大、小、增、减、纯，分别用在不同的音程上。
下面举例说明：
音数是0的“一度”叫做“纯一度”它们是同度。比如：C-C D-D E-E F-F G-G A-A B-B 。
谱例2：


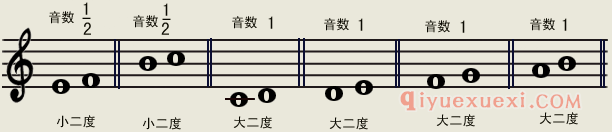
下面面紧接着是“小二度”，它的音数是1/2的小二度，而音数为1的二度叫“大二度”。在自然音阶里 E - F 、 B - C 是“小二度”（半音），其它两音相邻的音程关系都是“大二度”。
谱例3：

3 音程的标写
音程的度数要用阿拉伯数字标写。音数用大、小、增、减、纯、倍增、倍减来标写。比如：大六度就要写程“大6”，小二度要写成“小2”，纯五度就写成“纯5”，依次类推有这样一个规律：凡是二度、三度、六度音程，都用“大”“小”两个字来区分；而一度、四度、五度都用“纯”字。
1 自然音程
纯音程包括：纯一度、纯四度、纯五度、纯八度。
大音程包括：大二度、大三度、大六度、大七度。
小音程包括：小二度、小三度、小六度、小七度。
增四度、减五度 也叫“自然音程”。
2 变化音程
变化音程是由自然音程变化而来的。
大小音程是可以互相转换的。举一个例子：大六度音程，如果把把冠音降低半个音，或者将根音升高半个音，那末这个音程就从大六度变成了小六度。由此可以看得出，音程的度数是由两个音之间的距离来决定的，音程的性质（大、小、纯、增、减）是由它所含的音数决定的，这就是变化音程。
谱例：

音乐在人听起来由舒服和不舒服的区分。这是由于同时出现的音（也就是和声音程）有协和与不协和之分。协和的音程人们听起来就悦耳，而不协和的音程人们听起来就刺耳、很难听，有一种压迫感。听起来悦耳的音程是协和音程，听起来是刺耳的、不融和的音程就叫做不协和音程。
下面我们先谈谈协和音程：
协和音程一共有三种效果：
1 极完全协和音程：纯一度、 纯八度。
2 完全协和音程： 纯四度 、 纯五度。
3 不完全协和协和音程：小三度、大三度、小六度、大六度。
以上这三种音程的音响效果各有不同：
极完全协和的音程，听起来是一个音，或者是几乎是一个音的效果。（纯八度有一点空洞的感觉）。
完全协和音程，听起来是互相包容的，很舒服的感觉.
（不完全协和音程，听起来有一点跳的感觉，虽然如此却还可以容忍，所以也算在协和音程之内）。
4 不协和音程听起来就十分刺耳了，这种音程包括大二度、小二度、大七度、小七度、以及增减音程。
不协和音程使人的听觉受到刺激。但是在特定的情绪和条件时经常使用到这种不协和音程的，我们在音乐作品会常常听到它们。
单音程比较简单些，它是指在一个八度之内的音程，叫做单音程。超过一个八度之外的音程叫复音程。
单音程的称呼比较容易一些，是几度就可以直接称呼。比如大三度、纯八度、增二度、小七度等等。
复音程相对来讲就比较复杂一些。简单的办法可以用“加七”或“减七”的办法来算。
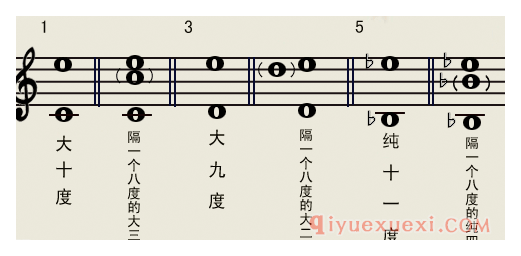
用“加七”的办法算是这样的：把现有的度数加上七度，然后一共是几度就直接称呼它的度数。（请看谱例1里的1、3、5、6）
用“减七”的办法算是这样的： 减去八度但是要称为“隔八度的多少度。下面举例：
谱例1：

音程的转位：就是把音程上下两个音的位置颠倒过来（根音和冠音互相倒置）上方音成为下方音，下方音成为上方音。这就是音程的换位。
音程转位可以在一个八度之内，也可以超过一个八度。
音程的转位可以单独移动根音和冠音，也可以将根音和冠音同时移位。
谱例1：


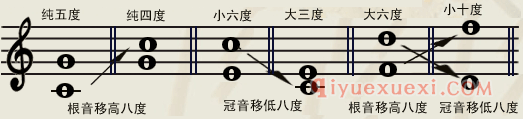
音程转位以后出现的现象：
（一）音程通过转位以后，除了改变它们之间的度数以外，还改变了它们之间的关系和种类。
1 首先是大音程经过转位以后，都变成了小音程，而小音程却成为了大音程。
2 增音程和倍增音程经过转位都变成了减音程和倍减音程。
下面我们看一个图表：

（二）音程转位以后改变了度数，计算的方法如下：
原位音程的度数和转位音程的度数的总和相加起来是九度。要计算转位音程的度数只要在九度里将原位音程的度数减掉，就是转位音程的度数。

还有一个办法是反过来。将原位的度数与转位的度数相加等于九，也是可以的。

依次类推。
（三） 音程转位以后不改变它们的性质，也就是说：协和音程经过转位仍然是协和音程，不协和音程还是不协和音程，不完全协和音程同样也是依旧。
（四）音程经过转位以后，单音程变成了复音程，而复音程则变成了单音程。